Chapitre 6 : Proportionnalité

    I. Situations de proportionnalité

    I.a. Reconnaître une situation de proportionnalité (rappels).

    Définition : un tableau est un tableau de proportionnalité lorsque tous les nombres d'une ligne s'obtiennent en multipliant tous ceux de l'autre ligne par un même nombre. Ce nombre est appelé coefficient de proportionnalité.

    ?

    Méthode : Pour reconnaître un tableau de proportionnalité, on effectue chacun des quotients d'un nombre de la seconde ligne du tableau par le nombre correspondant de la première ligne.

    Si tous les quotients sont égaux, le tableau est un tableau de proportionnalité ; sinon il ne l'est pas.

    Exemples :

    1. Ce tableau est un tableau de proportionnalité :
      En effet, 9/2=4,5, 13,5/3=4,5, 18/4=4,5
      Le coefficient de proportionnalité 4,5 signifie que 1kg d'oranges coûte 4,5€.

      Remarques :
      Le quotient commun est appelé coefficient de proportionnalité.

    2. Ce tableau n'est pas un tableau de proportionnalité :
      En effet, 100/5=20, 130/10=13, et 20 ≠ 13.

    Masses d'oranges (en kg) 2 3 4
     Prix (en €) 9 13,5 18
    Âge (en années)
    		 5 10
    Taille (en cm)
    		 100 130

    I.b. Déterminer une quatrième proportionnelle.

    Vocabulaire : Dans un tableau de proportionnalité, lorsque l'on connait trois nombres non nuls (dont deux se correspondent), on peut calculer le quatrième nombre manquant.
    Ce nombre est appelé le la quatrième proportionnelle.

    ?

    Méthodes : Calcul d'une quatrième proportionnelle.

     

    La quantité d'eau, en litres, qui s'écoule d'un robinet est proportionnelle à la durée, en minutes, de l'ouverture du robinet.
    Voici trois méthodes pour calculer le nombre manquant que l'on appellera m.

    • Coefficient de proportionnalité :
    4
    		 6
    12  m 

    m = 6 × 3 = 18

    • Multiplication d'une quantité :
    4
    		 6
    12  m 

    m = 12 × 1,5 = 18

    • Passage à l'unité :

    En 4 minutes il s'écoule 12L d'eau, donc en 1 minutes, il s'écoule 4 fois moins d'eau, soit 3L (12/4=3). En 6 minutes, il s'écoule 6 fois plus d'eau soit 18L (3 × 6 = 18).


    Conclusion : en 6 minutes, il s'écoule 18L d'eau.

    • Dernière méthode : produit en croix.
    4 6
    12  m 

    m = (12 × 6)/4 = (4 × 3 × 6)/ 4 = 3 × 6 = 18

    II. Proportionnalité et représentation graphique.

    Propriété :

    1. ⇒ Si une situation est une situation de proportionnalité, alors elle est représentée graphiquement par une droite passant par l’origine du repère.
    2. ⇐ Si une situation est représentée graphiquement par une droite passant par l’origine du repère, alors c'est une situation de proportionnalité.

    Exemples :

    1. Situation de proportionnalité

    Masses d'oranges

    (en kg)

    		2 3 4
     Prix (en €) 9 13,5 18

        2. Situations non proportionnelles

    Âge

    (en années)

    		1 3 10
     Taille (en cm) 86 94 135

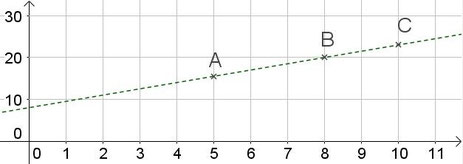
    Le tarif d’une bibliothèque comprend une carte à 8 euros pour l’année plus 1,5 euro par livre emprunté.

    Nombre de livres

    		5 8 10
     Dépense totale 15,5 20 23

    si et seulementsi

    ⇔

    si et seulement si

    ⇔

    si et seulement si

    ⇔

    les points sont alignés avec l'origine du repère (la droite passe par l'origine du repère).

    les points ne sont pas alignés avec l'origine du repère (la courbe n'est pas une droite).


    III. Applications de la proportionnalité.

    III.a. Pourcentages.

    Activité introductive

    Exemple :

     

    25 filles et 20 garçons de deux classes de 4ème ont effectué un devoir commun.

    60 % des filles et 50 % des garçons ont obtenu la moyenne.

    Calcule le pourcentage d'élèves qui ont obtenu la moyenne dans l'ensemble de ces deux classes.

     

    Résolution :

    1. Nombre de filles qui ont obtenu la moyenne :

      

    2. Nombre de garçons qui ont obtenu la moyenne :

    3. On calcule le nombre total d'élèves dans les deux classes : 25 + 20 = 45 élèves.

    On calcule le nombre d'élèves ayant eu la moyenne : 15 + 10 = 25 élèves.

    Nombre d'élèves qui ont obtenu la moyenne

    		5 n
    Nombre TOTAL d'élèves 45 100

    L'égalité des produits en croix donne :
    45 × n = 25 × 100

    D'où : 

    n ≈ 56

    Donc environ 56 % des élèves des deux classes ont obtenu la moyenne.

    III.b. Échelle.

    Définition : L'échelle du plan est le coefficient de proportionnalité entre les distances sur le plan et les distances réelles, exprimées dans la MÊME UNITÉ : 

    Télécharger
    Impression Guyane
    12 plans à coller dans le cours
    guyane.pdf
    Document Adobe Acrobat 18.9 KB
    Télécharger

    Exemple :

    1. Donner l'échelle de cette carte sous la forme d'une fraction .
    2. Quelle est la distance à vol d'oiseau entre Cayenne et Maripasoula ?
    3. La distance entre Cayenne et Paris est de 7074,295 km. Quelle serait la distance sur une carte à l'échelle  de ces deux villes ?

    1. On cherche à donner une échelle de la carte ci-contre. On prend la mesure sur la carte du segment blanc : 0,5cm. Donc 0,5cm sur la carte correspond à 50km dans la réalité.
      Mettons toutes les données dans la même unité ;
      -> 0,5cm
      -> 50km = 5 000 000cm
      Ainsi,est une échelle de la carte. Afin de mettre cette fraction sous la forme souhaitée, on multiplie le numérateur et le dénominateur de cette fraction par 2 :
    2. On cherche la distance à vol d'oiseau entre ces deux villes. Mesurons cette distance sur la carte : 3cm.
      Donc, si 1cm sur le plan correspond à 10 000 000cm en réalité, 3cm correspond à 30 000 000cm sur la carte, soit encore 300km.
    3.  Cette échelle signifie que 1cm sur le plan correspond à 39 300 000cm en réalité.
      7074,295 km = 707 429 500 cm
    Distance sur le plan (en cm) 1 18
     Distance réelle (en cm) 39 300 000  707 429 500

    Le tableau est un tableau de proportionnalité, on obtient donc environ 18cm.

    La distance entre Cayenne et Paris sera d'environ 18cm sur le plan.

    III.c. Vitesse. moyenne

    Définition : Un objet mobile parcourt une distance d pendant une durée t.
    La vitesse moyenne, notée v, de ce mobile est donnée par la formule :   v =.

    Remarque : 

    L'unité de la vitesse est donnée, la plupart du temps, en m/s ou en km/h. 
    Le seul fait de se rappeler de l'unité de la vitesse nous permet de nous retrouver cette formule. En effet, des km/h sont des kilomètres (km), soit une distance, divisés par de heures (h), soit une durée. Ainsi la vitesse est donné par la formule v =.

    Exemple :

    Énoncé : Une fourmi pressée marche à une vitesse de 3 mètres par minute. Donner la vitesse de la fourmi en m/s puis en km/h.

     

    On connait la formule de la vitesse,  v = et on sait qu'une fourmi parcours 3 mètres par minute.

    Ainsi, v =   =   =  =  =  = 0,05 m/s

     

    Une fourmi pressée a une vitesse de 0,05 m/s.

     

    v =  =  =   =  =  = 0,18 km/h

     

    Une fourmi pressée a une vitesse de 1,8 km/h.

     

    !

    Le produit en croix nous permet de donner d'autres égalités :

    • d = v × t