Chapitre 6 : Triangles
L'activité faite en groupe (avec les spaghettis) nous a laissé penser qu'avec trois longueurs données, on ne peut pas toujours construire un triangle (« les bouts ne se touchent pas »).
I. Construction de triangles.
I.a. Inégalité triangulaire.
Inégalité triangulaire (admise) : Quels que soient les points A, B et C, on a toujours .
Remarque :
Cette inégalité traduit le fait que la plus courte distance entre deux points est la ligne droite.
- Cas d'inégalité
Propriété : Dans un triangle, la somme des longueurs de deux côtés est supérieure à la longueur du troisième côté.
Exemples :
-
Dans un triangle ABC ;
AC + BC > AB
AB + BC > AC
AB + AC > BC
- Tracer un triangle DEF quelconque. Vérifier la propriété ci-dessus en mesurant chacun des côtés et en effectuant les sommes adéquates.
Conséquence :
Pour savoir s'il est possible de construire un triangle dont on donne les longueurs de trois côtés, il suffit de vérifier que la somme des deux plus petites longueurs est supérieure à la troisième longueur. Si la plus grande longueur est supérieure à la somme des deux autres, on ne peut pas construire le triangle.
- Cas d'égalité
Propriété :
– Si un point B appartient à un segment [AC], alors : AB + BC = AC
– Si A, B et C sont trois points tels que AB + BC = AC, alors B appartient au segment [AC].
Remarque :
Dans ce cas, on dit que ABC est un triangle aplati.
I.b.Construction de triangles.
On peut construire un triangle lorsque l'on connaît :
- La longueur d'un côté et les mesures des deux angles qui lui sont adjacent.
- Les longueurs de deux côtés et la mesure de l'angle compris entre ces deux côtés
- Les longueurs de trois côtés (dans le cas où la somme des deux petites longueurs est supérieures à la troisième longueur).
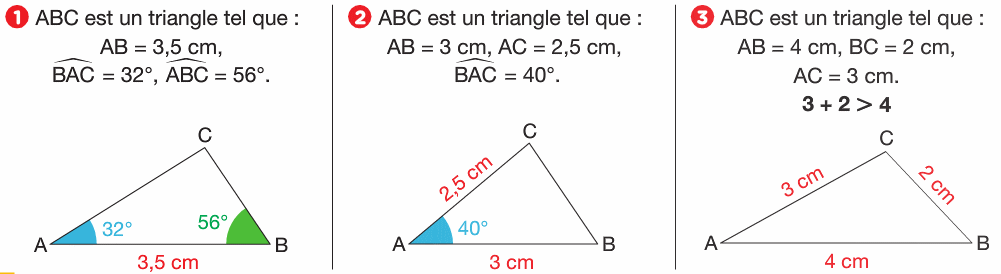
Exemples :
II. Rappels sur les tracés d'angles.
II.a. L'utilisation du rapporteur.
Afin de tracer ou de mesurer des angles pour un schéma ou un plan, ou pour construire un objet, on utilisera un rapporteur.
Comment mesurer un angle ou le construire avec un rapporteur ?
Un instrument pour les angles : le rapporteur.
Pour mesurer un angle, on utilise un rapporteur.
La plupart des rapporteurs sont gradués en degré (°) avec une double graduation :
• de 0 à 180° de gauche à droite sur la graduation extérieure ;
• et de 0 à 180° de droite à gauche sur la graduation intérieure.
Mesurer un angle avec un rapporteur.
Mesurer un angle avec le rapporteur.
- On fait coïncider le centre du rapporteur avec le sommet de l’angle.
2. On fait coïncider un des côtés avec le 0° d’une des graduations (ici, c’est la graduation intérieure).
3. On lit la mesure de l’angle sur la graduation correspondant au zéro (ici, il s’agit de la graduation intérieure).
On lit donc :
Tracer un angle avec le rapporteur
Tracer un angle de 40°.
1. On trace une demi-droite [OA).
2. On fait coïncider le sommet O de l’angle à tracer avec le centre du rapporteur.
3. On repère 40° sur la graduation correspondant au zéro (dans ce cas, il s’agit de la graduation intérieure).
4. On trace la demi-droite [OB).
II.b. Reporter un angle à l'aide du compas.
1. Je place deux points A et B n’importe où sur [Ox) et [Oy). Il suffit ensuite de reproduire le triangle OAB.
2. Je trace une demi-droite [O’x’) sur mon cahier. Je prends la longueur OA comme écartement de compas. Je pointe le compas sur l’origine de la demi-droite que je viens de tracer et trace un arc qui coupe [O’x’) en A’.
3. Je prends la longueur AB comme écartement de compas. Je pointe le compas en A’ et je trace un arc.
4. Je prends la longueur OB comme écartement de compas. Je pointe le compas sur O’ et je trace un arc qui coupe ce dernier tracé en B’. Je trace la demi-droite d’origine O’
qui passe par B’. et
ont la même mesure.
III. Somme des angles dans un triangle.
III.a. Cas général.
Propriété :
Dans un triangle, la somme des mesures des angles est égale à 180°.
Exemples :
-
Construire un triangle quelconque.
Donner la mesure de chacun de ses angles à l'aide du rapporteur.
Faire la somme de ces trois angles.
-
Le triangle BOL est tel que
= 45° et
= 60°.
Quelle est la mesure de l'angle ?
+
= 45° + 60° = 105°
Or, la somme des mesures des angles d'un triangle est égale à 180°.
Donc = 180° - 105° = 75°
III.b. Triangle isocèle.
Propriété :
Dans un triangle isocèle, les angles à la base ont même mesure.
Exemples :
Construire un triangle isocèle.
Donner la mesure de chacun de ses angles à l'aide du rapporteur.
Coder la figure.
III.c. Triangle équilatéral.
Propriété :
Dans un triangle équilatéral, tous les angles ont même mesure et valent 60°.
Exemples :
Construire un triangle équilatéral.
Donner la mesure de chacun de ses angles à l'aide du rapporteur.
Coder la figure.
III.d. Triangles rectangle et rectangle isocèle..
Propriété :
Dans un triangle rectangle, un angle mesure 90° (angle droit) et la somme des deux autres angles vaut 90°.
Vocabulaire : Lorsque la somme des mesures de deux angles vaut 90°, on dit que ces angles sont complémentaires.
Exemples :
-
Construire un triangle rectangle.
Donner la mesure de chacun de ses angles à l'aide du rapporteur.
Faire la somme des deux angles qui ne sont pas droits.
- Deux angles complémentaires.
Propriété :
Dans un triangle rectangle isocèle, un angle mesure 90° (angle droit) et les deux autres sont égaux et mesurent 45°.
Exemple :
Construire un triangle rectangle.
Donner la mesure de chacun de ses angles à l'aide du rapporteur.
Coder la figure