Chapitre 4 : prismes droits et cylindres
Les élèves découvrent les propriétés du prisme droit.
I. Prismes droits.
I.a. Description.
Définition : Un prisme droit est un solide qui possède deux bases qui sont des polygones superposables et dont les autres faces sont des rectangles.
Exemples :
1. On retrouve beaucoup d'objets en forme de prismes droits dans la vie courante.







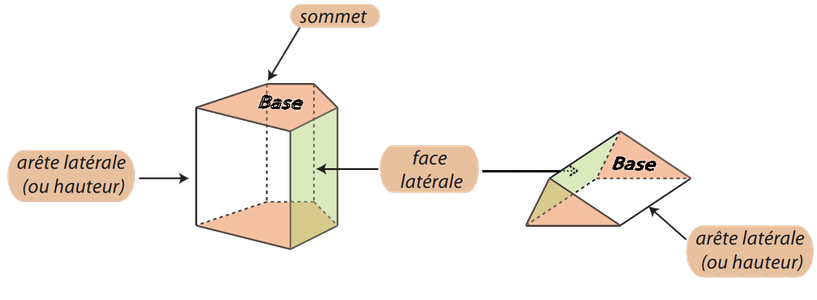
2. Quelques exemples en perspective cavalière.
Propriétés : Dans un prisme droit.
- Toutes les arêtes des faces latérales sont parallèles et ont la même longueur.
- Les arêtes des deux bases sont parallèles entre elles et ont la même longueur.
I.b. Perspective cavalière.
Propriétés : Lorsqu'on représente un solide en perspective cavalière :
- la face avant est représentée en vraie grandeur ;
- deux arêtes parallèles sont représentées par deux arêtes parallèles et deux arêtes sécantes par deux arêtes sécantes ;
- les arêtes cachées sont dessinées en pointillés tandis que les visibles sont en traits pleins.

I.c. Patron.
Lorsque l'on déplie un prisme droit, on obtient son patron.
Lorsque l'on plie le patron d’un prisme droit on obtient le prisme droit.
II. Cylindre de révolution.
II.a. Description.
Définition : Un cylindre de révolution est un solide qui a les caractéristiques suivantes :
-
deux faces superposables et parallèles qui sont des disques ; ces faces sont appelées bases du cylindre.
-
une surface latérale courbe qui, mise à plat, est un rectangle.
Le rayon des disques est le rayon du cylindre. La distance entre leurs centres est la hauteurdu cylindre.
Exemples :
1. On retrouve beaucoup d'objets en forme de prismes droits dans la vie courante.
2. Un cylindre de révolution en perspective cavalière.
Vocabulaire :
le mot révolution vient du latin volvere qui signifie « rouler ». La révolution d'un corps est la rotation de ce corps autour de son axe central.




II.b. Perspective cavalière.

II.c. Patron.
Définition : le périmètre P d'un cercle (aussi appelé circonférence) de rayon r est donné par la formule :
-
P = 2 × r × π
On sait que 2 × r est égal au diamètre d. Cette formule peut aussi s'écrire : - P = π × d
Méthode :
- Avant de commencer à tracer quoi que ce soit, on commence par calculer la circonférence du disque de base en utilisant la formule P = 2 × π × r (ou encore P = d× π).
- On trace ensuite un rectangle dont les dimensions correspondent à la hauteur du cylindre par la circonférence du disque de base.
- On trace ensuite les bases : deux disques de rayon le rayon du cylindre, placés sur chacun des côtés du rectangle correspondants à la circonférence du disque.