Chapitre 2 : Triangles
I. Définition.
Définition : Deux figures sont symétriques par rapport à une droite lorsqu'elles se superposent par pliage le long de cette droite.
Exemple :
Question : Les figures suivantes sont-elles symétriques par rapport à l'axe rouge (d) ?
Réponse : Les figures se superposent par pliage le long de l'axe rouge, elles sont donc symétriques.
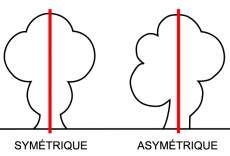
Définition : Une droite (d) est un axe de symétrie d'une figure si les deux parties de la figure se superposent par pliage le long de cette droite.
Exemples :

Remarques :
- Toutes les figures n'admettent pas forcément un axe de symétrie.
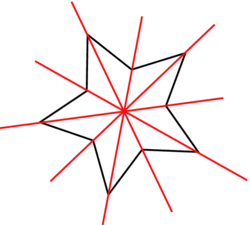
- Une figure peut admettre plusieurs axes de symétrie.
II. Propriétés de la symétrie axiale.
Propriétés : La symétrie axiale conserve :
- les distances ; dans une symétrie axiale, le symétrique d'un segment est un segment de même longueur.
- l'alignement ; dans une symétrie axiale, le symétrique d'une droite est une droite.
- les angles ; dans une symétrie axiale, le symétrique d'un angle est un angle de même mesure.
- les aires ; dans une symétrie axiale, deux figures symétriques sont superposables et ont donc la même aire.

Exemple :
Les triangles ABC et AB'C' sont symétriques par rapport à la droite (d) ;
- AB=AB' ; BC=B'C' ; CA=C'A
- M, A et C sont alignés, il en est de même pour leur symétrique M', A et C.
- ABC=90° et AB'C'=90°
- Les triangles ABC et AB'C' ont la même aire.
IV. Médiatrice d'un segment.
Remarque :
Si A' est le symétrique d'un point A par rapport à (Δ), alors on dit que (Δ) est la médiatrice du segment [AA'].
Définition : La médiatrice d'un segment est la droite perpendiculaire à ce segment, sécante en son milieu.
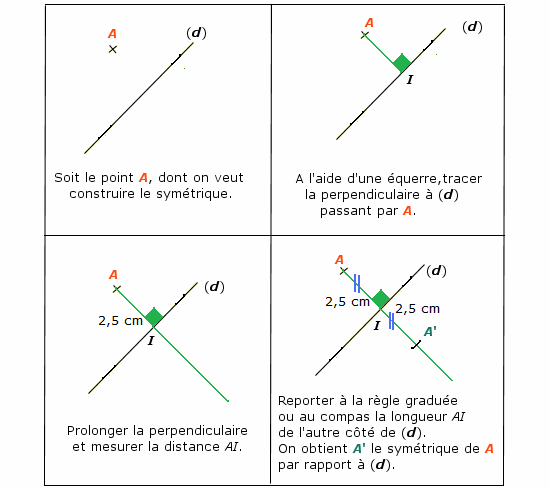
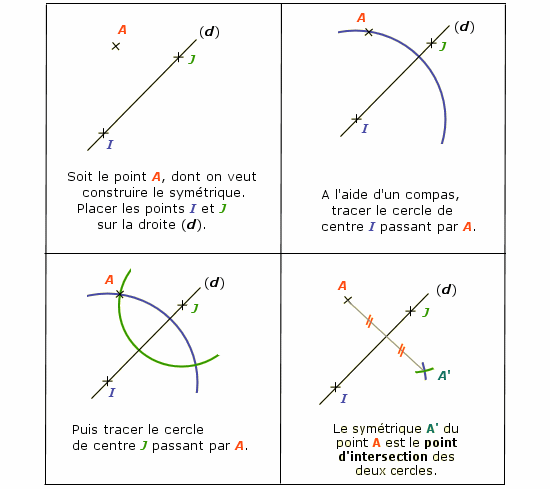
IV. Construction du symétrique d'un point par rapport à une droite.
Construire le symétrique A' (se lit « A prime ») d'un point A par rapport à une droite (d).
Méthode 1 : à l'équerre et au compas
Méthode 2 : au compas
VI. Symétrique des figures usuelles.
Pour tracer le symétrique :
- D'un segment, on cherche le symétrique de ses deux extrémités, puis on les relie.
Exercice : Tracer le symétrique du segment [AB] par rapport à la droite (d).
- D'une droite, on cherche le symétrique de deux points de la droite puis on les relie.
Exercice : Tracer le symétrique de la droite (AB) par rapport à la droite (d).
-
D'un cercle, on cherche le symétrique de son centre et on trace un cercle de même
rayon.
Exercice : Tracer le symétrique du cercle de centre O et de rayon 2cm par rapport à la droite (d).
-
D'un polygone, on cherche le symétrique de chacun de ses sommets puis on les relie dans le bon ordre.
Exercice : Tracer le symétrique du polygone ABC par rapport à la droite (d).